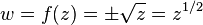Complex Plane - Gluing The Cut Plane Back Together

Gluing The Cut Plane Back Together

We have already seen how the relationship

can be made into a single-valued function by splitting the domain of f into two disconnected sheets. It is also possible to "glue" those two sheets back together to form a single Riemann surface on which f(z) = z1/2 can be defined as a holomorphic function whose image is the entire w-plane (except for the point w = 0). Here's how that works.

Imagine two copies of the cut complex plane, the cuts extending along the positive real axis from z = 0 to the point at infinity. On one sheet define 0 ≤ arg(z) < 2π, so that 11/2 = e0 = 1, by definition. On the second sheet define 2π ≤ arg(z) < 4π, so that 11/2 = eiπ = −1, again by definition. Now flip the second sheet upside down, so the imaginary axis points in the opposite direction of the imaginary axis on the first sheet, with both real axes pointing in the same direction, and "glue" the two sheets together (so that the edge on the first sheet labeled "θ = 0" is connected to the edge labeled "θ < 4π" on the second sheet, and the edge on the second sheet labeled "θ = 2π" is connected to the edge labeled "θ < 2π" on the first sheet). The result is the Riemann surface domain on which f(z) = z1/2 is single-valued and holomorphic (except when z = 0).

To understand why f is single-valued in this domain, imagine a circuit around the unit circle, starting with z = 1 on the first sheet. When 0 ≤ θ < 2π we are still on the first sheet. When θ = 2π we have crossed over onto the second sheet, and are obliged to make a second complete circuit around the branch point z = 0 before returning to our starting point, where θ = 4π is equivalent to θ = 0, because of the way we glued the two sheets together. In other words, as the variable z makes two complete turns around the branch point, the image of z in the w-plane traces out just one complete circle.

Formal differentiation shows that

from which we can conclude that the derivative of f exists and is finite everywhere on the Riemann surface, except when z = 0 (that is, f is holomorphic, except when z = 0).

How can the Riemann surface for the function

also discussed above, be constructed? Once again we begin with two copies of the z-plane, but this time each one is cut along the real line segment extending from z = −1 to z = 1 – these are the two branch points of g(z). We flip one of these upside down, so the two imaginary axes point in opposite directions, and glue the corresponding edges of the two cut sheets together. We can verify that g is a single-valued function on this surface by tracing a circuit around a circle of unit radius centered at z = 1. Commencing at the point z = 2 on the first sheet we turn halfway around the circle before encountering the cut at z = 0. The cut forces us onto the second sheet, so that when z has traced out one full turn around the branch point z = 1, w has taken just one-half of a full turn, the sign of w has been reversed (since eiπ = −1), and our path has taken us to the point z = 2 on the second sheet of the surface. Continuing on through another half turn we encounter the other side of the cut, where z = 0, and finally reach our starting point (z = 2 on the first sheet) after making two full turns around the branch point.

The natural way to label θ = arg(z) in this example is to set −π < θ ≤ π on the first sheet, with π < θ ≤ 3π on the second. The imaginary axes on the two sheets point in opposite directions so that the counterclockwise sense of positive rotation is preserved as a closed contour moves from one sheet to the other (remember, the second sheet is upside down). Imagine this surface embedded in a three-dimensional space, with both sheets parallel to the xy-plane. Then there appears to be a vertical hole in the surface, where the two cuts are joined together. What if the cut is made from z = −1 down the real axis to the point at infinity, and from z = 1, up the real axis until the cut meets itself? Again a Riemann surface can be constructed, but this time the "hole" is horizontal. Topologically speaking, both versions of this Riemann surface are equivalent – they are orientable two-dimensional surfaces of genus one.