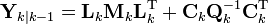Kalman Filter - Information Filter

Information Filter

In the information filter, or inverse covariance filter, the estimated covariance and estimated state are replaced by the information matrix and information vector respectively. These are defined as:

Similarly the predicted covariance and state have equivalent information forms, defined as:

as have the measurement covariance and measurement vector, which are defined as:

The information update now becomes a trivial sum.

The main advantage of the information filter is that N measurements can be filtered at each timestep simply by summing their information matrices and vectors.

To predict the information filter the information matrix and vector can be converted back to their state space equivalents, or alternatively the information space prediction can be used.

\textbf{M}_{k} = ^{\text{T}} \textbf{Y}_{k-1|k-1} \textbf{F}_{k}^{-1}
\textbf{C}_{k} = \textbf{M}_{k} ^{-1}
\textbf{L}_{k} = I - \textbf{C}_{k}
\textbf{Y}_{k|k-1} = \textbf{L}_{k} \textbf{M}_{k} \textbf{L}_{k}^{\text{T}} + \textbf{C}_{k} \textbf{Q}_{k}^{-1} \textbf{C}_{k}^{\text{T}}
\hat{\textbf{y}}_{k|k-1} = \textbf{L}_{k} ^{\text{T}}\hat{\textbf{y}}_{k-1|k-1}

Note that if F and Q are time invariant these values can be cached. Note also that F and Q need to be invertible.

Read more about this topic:  Kalman Filter

Famous quotes containing the word information:

    “So while it is true that children are exposed to more information and a greater variety of experiences than were children of the past, it does not follow that they automatically become more sophisticated. We always know much more than we understand, and with the torrent of information to which young people are exposed, the gap between knowing and understanding, between experience and learning, has become even greater than it was in the past.”
    —David Elkind (20th century)