Column Space - Basis

Basis

The columns of A span the column space, but they may not form a basis if the column vectors are not linearly independent. Fortunately, elementary row operations do not affect the dependence relations between the column vectors. This makes it possible to use row reduction to find a basis for the column space.

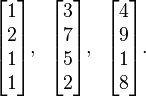
For example, consider the matrix

The columns of this matrix span the column space, but they may not be linearly independent, in which case some subset of them will form a basis. To find this basis, we reduce A to reduced row echelon form:

\begin{bmatrix} 1 & 3 & 1 & 4 \\ 2 & 7 & 3 & 9 \\ 1 & 5 & 3 & 1 \\ 1 & 2 & 0 & 8 \end{bmatrix} \sim \begin{bmatrix} 1 & 3 & 1 & 4 \\ 0 & 1 & 1 & 1 \\ 0 & 2 & 2 & -3 \\ 0 & -1 & -1 & 4 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -2 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & -5 \\ 0 & 0 & 0 & 5 \end{bmatrix} \sim \begin{bmatrix} 1 & 0 & -2 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}\text{.}

At this point, it is clear that the first, second, and fourth columns are linearly independent, while the third column is a linear combination of the first two. (Specifically, v3 = –2v1 + v2.) Therefore, the first, second, and fourth columns of the original matrix are a basis for the column space:

\begin{bmatrix} 1 \\ 2 \\ 1 \\ 1\end{bmatrix},\;\; \begin{bmatrix} 3 \\ 7 \\ 5 \\ 2\end{bmatrix},\;\; \begin{bmatrix} 4 \\ 9 \\ 1 \\ 8\end{bmatrix}\text{.}

Note that the independent columns of the reduced row echelon form are precisely the columns with pivots. This makes it possible to determine which columns are linearly independent by reducing only to echelon form.

The above algorithm can be used in general to find the dependence relations between any set of vectors, and to pick out a basis from any spanning set. A different algorithm for finding a basis from a spanning set is given in the row space article; finding a basis for the column space of A is equivalent to finding a basis for the row space of the transpose matrix AT.

Read more about this topic:  Column Space

Famous quotes containing the word basis:

    “Painting dissolves the forms at its command, or tends to; it melts them into color. Drawing, on the other hand, goes about resolving forms, giving edge and essence to things. To see shapes clearly, one outlines them—whether on paper or in the mind. Therefore, Michelangelo, a profoundly cultivated man, called drawing the basis of all knowledge whatsoever.”
    —Alexander Eliot (b. 1919)

    “Self-alienation is the source of all degradation as well as, on the contrary, the basis of all true elevation. The first step will be a look inward, an isolating contemplation of our self. Whoever remains standing here proceeds only halfway. The second step must be an active look outward, an autonomous, determined observation of the outer world.”
    —Novalis [Friedrich Von Hardenberg] (1772–1801)

    “Most young black females learn to be suspicious and critical of feminist thinking long before they have any clear understanding of its theory and politics.... Without rigorously engaging feminist thought, they insist that racial separatism works best. This attitude is dangerous. It not only erases the reality of common female experience as a basis for academic study; it also constructs a framework in which differences cannot be examined comparatively.”
    —bell hooks (b. c. 1955)