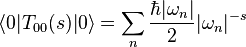Zeta Function Regularization - Example

Example

An example of zeta-function regularization is the calculation of the vacuum expectation value of the energy of a particle field in quantum field theory. More generally, the zeta-function approach can be used to regularize the whole energy-momentum tensor in curved spacetime.

The unregulated value of the energy is given by a summation over the zero-point energy of all of the excitation modes of the vacuum:

Here, is the zero'th component of the energy-momentum tensor and the sum (which may be an integral) is understood to extend over all (positive and negative) energy modes ; the absolute value reminding us that the energy is taken to be positive. This sum, as written, is usually infinite ( is typically linear in n). The sum may be regularized by writing it as

where s is some parameter, taken to be a complex number. For large, real s greater than 4 (for three-dimensional space), the sum is manifestly finite, and thus may often be evaluated theoretically.

Such a sum will typically have a pole at s = 4, due to the bulk contributions of the quantum field in three space dimensions. However, it may be analytically continued to s=0 where hopefully there is no pole, thus giving a finite value to the expression. A detailed example of this regularization at work is given in the article on the Casimir effect, where the resulting sum is very explicitly the Riemann zeta-function (and where the seemingly legerdemain analytic continuation removes an additive infinity, leaving a physically significant finite number).

The zeta-regularization is useful as it can often be used in a way such that the various symmetries of the physical system are preserved. Besides the Casimir effect, zeta-function regularization is used in conformal field theory, renormalization and in fixing the critical spacetime dimension of string theory.