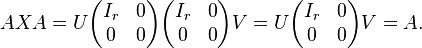Von Neumann Regular Ring - Examples

Examples

Every field (and every skew field) is von Neumann regular: for a≠0 we can take x = a -1. An integral domain is von Neumann regular if and only if it is a field.

Another example of a von Neumann regular ring is the ring Mn(K) of n-by-n square matrices with entries from some field K. If r is the rank of A∈Mn(K), then there exist invertible matrices U and V such that

A = U \begin{pmatrix}I_r &0\\ 0 &0\end{pmatrix} V

(where Ir is the r-by-r identity matrix). If we set X = V -1U -1, then

AXA= U \begin{pmatrix}I_r &0\\ 0 &0\end{pmatrix} \begin{pmatrix}I_r &0\\ 0 &0\end{pmatrix} V = U \begin{pmatrix}I_r &0\\ 0 &0\end{pmatrix} V = A.

More generally, the matrix ring over a von Neumann regular ring is again a von Neumann regular ring.

The ring of affiliated operators of a finite von Neumann algebra is von Neumann regular.

A Boolean ring is a ring in which every element satisfies a2 = a. Every Boolean ring is von Neumann regular.

Read more about this topic:  Von Neumann Regular Ring

Famous quotes containing the word examples:

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)