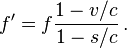Velocity-addition Formula - Doppler Shift

Doppler Shift

A notion of velocity addition can also be formulated in the theory of the nonrelativistic, one dimensional Doppler shift. When the source of a wave is moving with nonrelativistic velocity s toward the receiver, the frequency of the waves is increased by a factor of 1/(1 − s/c). If the receiver is moving with velocity v, the frequency of the waves detected is decreased by a factor of (1 − v/c). When both the source and the receiver are moving, the frequency measured is given by:

If a receiver measures velocities using Doppler shifts, and it determines that an object coming towards it is moving with velocity u, it is actually determining the shift in frequency, from which it calculates the velocity. Suppose that the receiver itself is moving with velocity v, but it does not take this into account in the calculation. It calculates the value u falsely assuming that it is at rest. The velocity u can then be thought of as the inferred velocity relative to the ship from Doppler shifts alone. What, then, is the actual velocity of the object relative to the medium?

Since the ship determined u from the frequency, the frequency shift factor relative to the ship is

But this factor is not the frequency shift relative to a stationary receiver. For a stationary observer, it must be corrected by dividing by the frequency shift of the ship:

The velocity of the object relative to the medium is then given by

This is the true velocity of the object. Unlike the relativistic addition formula, the velocity u is not the physical velocity of the object.

There is a group of transformations in one space and one time dimension for which this operation forms the addition law. The group is defined by all matrices:

When they act on, they produce the transformations

which is a Galilean boost accompanied by a rescaling of the x coordinate. When two of these matrices are multiplied, the quantity v (the velocity of the frame), combines according to the Doppler addition law.

The physical meaning can be extracted from the transformation. Time is the same for both frames, but the rescaling of the x axis keeps the right-moving speed of sound fixed in the moving frame. This means that if the ship uses this transformation to define its frame, the ruler that it uses is the distance that the waves move to the right in one unit of time. The velocity u can now be given a physical interpretation, although an unusual one. It is the velocity of the object as measured from the ship using a Doppler contracted ruler.