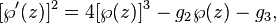Riemann Surface - Analytic Vs. Algebraic

Analytic Vs. Algebraic

The above fact about existence of nonconstant meromorphic functions can be used to show that any compact Riemann surface is a projective variety, i.e. can be given by polynomial equations inside a projective space. Actually, it can be shown that every compact Riemann surface can be embedded into complex projective 3-space. This is a surprising theorem: Riemann surfaces are given by locally patching charts. If one global condition, namely compactness, is added, the surface is necessarily algebraic. This feature of Riemann surfaces allows to study them with either the means of analytic or algebraic geometry. The corresponding statement for higher-dimensional objects is false, i.e. there are compact complex 2-manifolds which are not algebraic. On the other hand, every projective complex manifold is necessarily algebraic, see Chow's theorem.

As an example, consider the torus T := C/(Z + τ Z). The Weierstrass function belonging to the lattice Z + τ Z is a meromorphic function on T. This function and its derivative generate the function field of T. There is an equation

^2=4^3-g_2\wp(z)-g_3,

where the coefficients g2 and g3 depend on τ, thus giving an elliptic curve Eτ in the sense of algebraic geometry. Reversing this is accomplished by the j-invariant j(E), which can be used to determine τ and hence a torus.

Read more about this topic:  Riemann Surface

Famous quotes containing the words analytic and/or algebraic:

    ““You, that have not lived in thought but deed,
    Can have the purity of a natural force,
    But I, whose virtues are the definitions
    Of the analytic mind, can neither close
    The eye of the mind nor keep my tongue from speech.””
    —William Butler Yeats (1865–1939)

    “I have no scheme about it,—no designs on men at all; and, if I had, my mode would be to tempt them with the fruit, and not with the manure. To what end do I lead a simple life at all, pray? That I may teach others to simplify their lives?—and so all our lives be simplified merely, like an algebraic formula? Or not, rather, that I may make use of the ground I have cleared, to live more worthily and profitably?”
    —Henry David Thoreau (1817–1862)