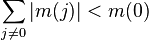Positive-definite Matrix - Further Properties

Further Properties

If M is an Hermitian positive-semidefinite matrix, one sometimes writes M ≥ 0 and if M is positive-definite one writes M > 0. The notion comes from functional analysis where positive-semidefinite matrices define positive operators.

For arbitrary square matrices M,N we write M ≥ N if M − N ≥ 0; i.e., M − N is positive semi-definite. This defines a partial ordering on the set of all square matrices. One can similarly define a strict partial ordering M > N.

1. Every positive definite matrix is invertible and its inverse is also positive definite. If M ≥ N > 0 then N−1 ≥ M−1 > 0.
2. If M is positive definite and r > 0 is a real number, then r M is positive definite. If M and N are positive definite, then the sum M + N and the products MNM and NMN are also positive definite. If MN = NM, then MN is also positive definite.
3. If M,N ≥ 0, although MN is not necessary positive-semidefinite, the Kronecker product M ⊗ N ≥ 0, the Hadamard product M ○ N ≥ 0 (this result is often called the Schur product theorem)., and the Frobenius product Frobenius product M : N ≥ 0 (Lancaster-Tismenetsky, The Theory of Matrices, p. 218).
4. Regarding the Hadamard product of two positive-semidefinite matrices M = (m_ij) ≥ 0, N ≥ 0, there are two notable inequalities:

   (Oppenheim's inequality)

5. A matrix M is positive semi-definite if and only if there is a positive semi-definite matrix B with B2 = M. This matrix B is unique, is called the square root of M, and is denoted with B = M1/2 (the square root B is not to be confused with the matrix L in the Cholesky factorization M = LL*, which is also sometimes called the square root of M). If M > N > 0 then M1/2 > N1/2 > 0.
6. If M = (m_ij) ≥ 0 then the diagonal entries m_ii are real and non-negative. As a consequence the trace, tr(M) ≥ 0. Furthermore

   and thus

7. If is a symmetric matrix of the form, and the strict inequality holds

   

   then is strictly positive definite.
8. Let M > 0 and N Hermitian. If MN + NM ≥ 0 (resp., MN + NM > 0) then N ≥ 0 (resp., N > 0).
9. If M > 0 is real, then there is a δ > 0 such that M > δI, where I is the identity matrix.
10. The set of positive semidefinite symmetric matrices is convex. That is, if M and N are positive semidefinite, then for any between 0 and 1, is also positive semidefinite. For any vector x:
    This property guarantees that semidefinite programming problems converge to a globally optimal solution.