Multivariate Normal Distribution - Marginal Distributions

Marginal Distributions

To obtain the marginal distribution over a subset of multivariate normal random variables, one only needs to drop the irrelevant variables (the variables that one wants to marginalize out) from the mean vector and the covariance matrix. The proof for this follows from the definitions of multivariate normal distributions and linear algebra.

Example

Let x = be multivariate normal random variables with mean vector μ = and covariance matrix Σ (standard parametrization for multivariate normal distributions). Then the joint distribution of x′ = is multivariate normal with mean vector μ′ = and covariance matrix 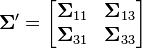$\boldsymbol\Sigma' = \begin{bmatrix} \boldsymbol\Sigma_{11} & \boldsymbol\Sigma_{13} \\ \boldsymbol\Sigma_{31} & \boldsymbol\Sigma_{33} \end{bmatrix}$ .

Read more about this topic: Multivariate Normal Distribution

Famous quotes containing the word marginal:

“Of course I’m a black writer.... I’m not just a black writer, but categories like black writer, woman writer and Latin American writer aren’t marginal anymore. We have to acknowledge that the thing we call “literature” is more pluralistic now, just as society ought to be. The melting pot never worked. We ought to be able to accept on equal terms everybody from the Hassidim to Walter Lippmann, from the Rastafarians to Ralph Bunche.”
—Toni Morrison (b. 1931)