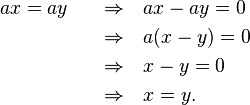Multiplicative Inverse - Further Remarks

Further Remarks

If the multiplication is associative, an element x with a multiplicative inverse cannot be a zero divisor (meaning for some y, xy = 0 with neither x nor y equal to zero). To see this, it is sufficient to multiply the equation xy = 0 by the inverse of x (on the left), and then simplify using associativity. In the absence of associativity, the sedenions provide a counterexample.

The converse does not hold: an element which is not a zero divisor is not guaranteed to have a multiplicative inverse. Within Z, all integers except −1, 0, 1 provide examples; they are not zero divisors nor do they have inverses in Z. If the ring or algebra is finite, however, then all elements a which are not zero divisors do have a (left and right) inverse. For, first observe that the map ƒ(x) = ax must be injective: ƒ(x) = ƒ(y) implies x = y:

\begin{align} ax &= ay &\quad \rArr & \quad ax-ay = 0 \\ & &\quad \rArr &\quad a(x-y) = 0 \\ & &\quad \rArr &\quad x-y = 0 \\ & &\quad \rArr &\quad x = y. \end{align}

Distinct elements map to distinct elements, so the image consists of the same finite number of elements, and the map is necessarily surjective. Specifically, ƒ (namely multiplication by a) must map some element x to 1, ax = 1, so that x is an inverse for a.

The multiplicative inverse of a fraction is simply

Read more about this topic:  Multiplicative Inverse

Famous quotes containing the word remarks:

    “Where do whites fit in the New Africa? Nowhere, I’m inclined to say ... and I do believe that it is true that even the gentlest and most westernised Africans would like the emotional idea of the continent entirely without the complication of the presence of the white man for a generation or two. But nowhere, as an answer for us whites, is in the same category as remarks like What’s the use of living? in the face of the threat of atomic radiation. We are living; we are in Africa.”
    —Nadine Gordimer (b. 1923)

    “An illustrious individual remarks that Mrs. [Elizabeth Cady] Stanton is the salt, Anna Dickinson the pepper, and Miss [Susan B.] Anthony the vinegar of the Female Suffrage movement. The very elements get the “white male” into a nice pickle.”
    —Anonymous, U.S. women’s magazine contributor. The Revolution (August 19, 1869)