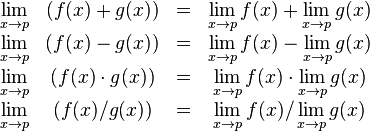Limit of A Function - Properties

Properties

If a function f is real-valued, then the limit of f at p is L if and only if both the right-handed limit and left-handed limit of f at p exist and are equal to L.

The function f is continuous at p if and only if the limit of f(x) as x approaches p exists and is equal to f(p). If f : M → N is a function between metric spaces M and N, then it is equivalent that f transforms every sequence in M which converges towards p into a sequence in N which converges towards f(p).

If N is a normed vector space, then the limit operation is linear in the following sense: if the limit of f(x) as x approaches p is L and the limit of g(x) as x approaches p is P, then the limit of f(x) + g(x) as x approaches p is L + P. If a is a scalar from the base field, then the limit of af(x) as x approaches p is aL.

If f is a real-valued (or complex-valued) function, then taking the limit is compatible with the algebraic operations, provided the limits on the right sides of the equations below exist (the last identity only holds if the denominator is non-zero). This fact is often called the algebraic limit theorem.

In each case above, when the limits on the right do not exist, or, in the last case, when the limits in both the numerator and the denominator are zero, nonetheless the limit on the left, called an indeterminate form, may still exist—this depends on the functions f and g. These rules are also valid for one-sided limits, for the case p = ±∞, and also for infinite limits using the rules

• q + ∞ = ∞ for q ≠ −∞
• q × ∞ = ∞ if q > 0
• q × ∞ = −∞ if q < 0
• q / ∞ = 0 if q ≠ ± ∞

(see extended real number line).

Note that there is no general rule for the case q / 0; it all depends on the way 0 is approached. Indeterminate forms—for instance, 0/0, 0×∞, ∞−∞, and ∞/∞—are also not covered by these rules, but the corresponding limits can often be determined with L'Hôpital's rule or the Squeeze theorem.