Group Homomorphism - Examples

Examples

  • Consider the cyclic group Z/3Z = {0, 1, 2} and the group of integers Z with addition. The map h : Z → Z/3Z with h(u) = u mod 3 is a group homomorphism. It is surjective and its kernel consists of all integers which are divisible by 3.
  • Consider and group 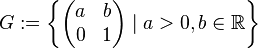G:=\left\{\begin{pmatrix} a & b \\ 0 & 1 \end{pmatrix}\mid a>0,b\in\mathbb{R}\right\} with . then functions of the form
s.t. f_u \left(\begin{pmatrix} a & b \\ 0 & 1 \end{pmatrix}\right)=a^u are group homomorphisms.
  • Consider multiplicative group of positive real numbers with then functions of the form
s.t. are group homomorphisms.
  • The exponential map yields a group homomorphism from the group of real numbers R with addition to the group of non-zero real numbers R* with multiplication. The kernel is {0} and the image consists of the positive real numbers.
  • The exponential map also yields a group homomorphism from the group of complex numbers C with addition to the group of non-zero complex numbers C* with multiplication. This map is surjective and has the kernel { 2πki : k in Z }, as can be seen from Euler's formula. Fields like R and C that have homomorphisms from their additive group to their multiplicative group are thus called exponential fields.

Read more about this topic:  Group Homomorphism

Famous quotes containing the word examples:

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)

    “No rules exist, and examples are simply life-savers answering the appeals of rules making vain attempts to exist.”
    —André Breton (1896–1966)

    “It is hardly to be believed how spiritual reflections when mixed with a little physics can hold people’s attention and give them a livelier idea of God than do the often ill-applied examples of his wrath.”
    —G.C. (Georg Christoph)