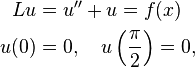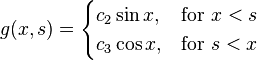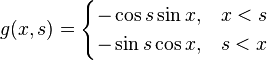Green's Function - Example

Example

Given the problem,

\begin{align} Lu & = u'' + u = f(x)\\ u(0)& = 0, \quad u\left(\dfrac{\pi}{2}\right) = 0, \end{align}

find the Green's function.

First step: The Green's function for the linear operator at hand is defined as the solution to

If, then the delta function gives zero, and the general solution is

For, the boundary condition at implies

The equation of is skipped because if and

For, the boundary condition at implies

The equation of is skipped for similar reasons.

To summarize the results thus far:

g(x,s)= \begin{cases} c_2 \sin x, & \text{for }x<s\\ c_3 \cos x, & \text{for }s<x \end{cases}

Second step: The next task is to determine and .

Ensuring continuity in the Green's function at implies

One can also ensure proper discontinuity in the first derivative by integrating the defining differential equation from to and taking the limit as goes to zero:

The two (dis)continuity equations can be solved for and to obtain

So the Green's function for this problem is:

g(x,s)=\begin{cases} -\cos s \sin x, & x<s\\ -\sin s \cos x, & s<x \end{cases}

Read more about this topic:  Green's Function

Famous quotes containing the word example:

    “Our intellect is not the most subtle, the most powerful, the most appropriate, instrument for revealing the truth. It is life that, little by little, example by example, permits us to see that what is most important to our heart, or to our mind, is learned not by reasoning but through other agencies. Then it is that the intellect, observing their superiority, abdicates its control to them upon reasoned grounds and agrees to become their collaborator and lackey.”
    —Marcel Proust (1871–1922)