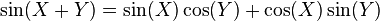Formal Power Series - Applications

Applications

Formal power series can be used to solve recurrences occurring in number theory and combinatorics. For an example involving finding a closed form expression for the Fibonacci numbers, see the article on Examples of generating functions.

One can use formal power series to prove several relations familiar from analysis in a purely algebraic setting. Consider for instance the following elements of Q]:

$\sin(X) := \sum_{n \ge 0} \frac{(-1)^n} {(2n+1)!} X^{2n+1}$

$\cos(X) := \sum_{n \ge 0} \frac{(-1)^n} {(2n)!} X^{2n}$

Then one can show that

$\sin^2(X) + \cos^2(X) = 1 \,$

and

$\frac{\partial}{\partial X} \sin(X) = \cos(X)$

as well as

$\sin (X+Y) = \sin(X) \cos(Y) + \cos(X) \sin(Y)\,$

(the latter being valid in the ring Q]).

In algebra, the ring K] (where K is a field) is often used as the "standard, most general" complete local ring over K.

Read more about this topic: Formal Power Series