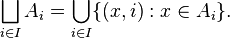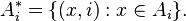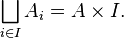Disjoint Union - Set Theory Definition

Set Theory Definition

Formally, let {A_i : i ∈ I} be a family of sets indexed by I. The disjoint union of this family is the set

$\bigsqcup_{i\in I}A_i = \bigcup_{i\in I}\{(x,i) : x \in A_i\}.$

The elements of the disjoint union are ordered pairs (x, i). Here i serves as an auxiliary index that indicates which A_i the element x came from.

Each of the sets A_i is canonically isomorphic to the set

$A_i^* = \{(x,i) : x \in A_i\}.$

Through this isomorphism, one may consider that A_i is canonically embedded in the disjoint union. For i ≠ j, the sets A_i* and A_j* are disjoint even if the sets A_i and A_j are not.

In the extreme case where each of the A_i are equal to some fixed set A for each i ∈ I, the disjoint union is the Cartesian product of A and I:

$\bigsqcup_{i\in I}A_i = A \times I.$

One may occasionally see the notation

$\sum_{i\in I}A_i$

for the disjoint union of a family of sets, or the notation A + B for the disjoint union of two sets. This notation is meant to be suggestive of the fact that the cardinality of the disjoint union is the sum of the cardinalities of the terms in the family. Compare this to the notation for the Cartesian product of a family of sets.

Disjoint unions are also sometimes written or .

In the language of category theory, the disjoint union is the coproduct in the category of sets. It therefore satisfies the associated universal property. This also means that the disjoint union is the categorical dual of the Cartesian product construction. See coproduct for more details.

For many purposes, the particular choice of auxiliary index is unimportant, and in a simplifying abuse of notation, the indexed family can be treated simply as a collection of sets. In this case is referred to as a copy of and the notation is sometimes used.

Read more about this topic: Disjoint Union

Famous quotes containing the words set, theory and/or definition:

“The poverty of our century is unlike that of any other. It is not, as poverty was before, the result of natural scarcity, but of a set of priorities imposed upon the rest of the world by the rich. Consequently, the modern poor are not pitied ... but written off as trash. The twentieth-century consumer economy has produced the first culture for which a beggar is a reminder of nothing.”
—John Berger (b. 1926)

“Freud was a hero. He descended to the “Underworld” and met there stark terrors. He carried with him his theory as a Medusa’s head which turned these terrors to stone.”
—R.D. (Ronald David)

“Perhaps the best definition of progress would be the continuing efforts of men and women to narrow the gap between the convenience of the powers that be and the unwritten charter.”
—Nadine Gordimer (b. 1923)