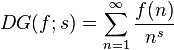Dirichlet Convolution - Dirichlet Series

Dirichlet Series

If f is an arithmetic function, one defines its Dirichlet series generating function by

DG(f;s) = \sum_{n=1}^\infty \frac{f(n)}{n^s}

for those complex arguments s for which the series converges (if there are any). The multiplication of Dirichlet series is compatible with Dirichlet convolution in the following sense:

DG(f;s) DG(g;s) = DG(f*g;s)\,

for all s for which both series of the left hand side converge, one of them at least converging absolutely (note that simple convergence of both series of the left hand side DOES NOT imply convergence of the right hand side!). This is akin to the convolution theorem if one thinks of Dirichlet series as a Fourier transform.

Read more about this topic:  Dirichlet Convolution

Famous quotes containing the word series:

    “I thought I never wanted to be a father. A child seemed to be a series of limitations and responsibilities that offered no reward. But when I experienced the perfection of fatherhood, the rest of the world remade itself before my eyes.”
    —Kent Nerburn (20th century)