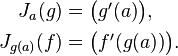Chain Rule - The Chain Rule in Higher Dimensions

The Chain Rule in Higher Dimensions

The simplest generalization of the chain rule to higher dimensions uses the total derivative. The total derivative is a linear transformation that captures how the function changes in all directions. Let f : Rm → Rk and g : Rn → Rm be differentiable functions, and let D be the total derivative operator. If a is a point in Rn, then the higher dimensional chain rule says that:

or for short,

In terms of Jacobian matrices, the rule says

That is, the Jacobian of the composite function is the product of the Jacobians of the composed functions. The higher-dimensional chain rule can be proved using a technique similar to the second proof given above.

The higher-dimensional chain rule is a generalization of the one-dimensional chain rule. If k, m, and n are 1, so that f : R → R and g : R → R, then the Jacobian matrices of f and g are 1 × 1. Specifically, they are:

\begin{align} J_a(g) &= \begin{pmatrix} g'(a) \end{pmatrix}, \\ J_{g(a)}(f) &= \begin{pmatrix} f'(g(a)) \end{pmatrix}. \end{align}

The Jacobian of f ∘ g is the product of these 1 × 1 matrices, so it is f′(g(a))g′(a), as expected from the one-dimensional chain rule. In the language of linear transformations, Da(g) is the function which scales a vector by a factor of g′(a) and Dg(a)(f) is the function which scales a vector by a factor of f′(g(a)). The chain rule says that the composite of these two linear transformations is the linear transformation Da(f ∘ g), and therefore it is the function that scales a vector by f′(g(a))g′(a).

Another way of writing the chain rule is used when f and g are expressed in terms of their components as y = f(u) = (f1(u), ..., fk(u)) and u = g(x) = (g1(x), ..., gm(x)). In this case, the above rule for Jacobian matrices is usually written as:

The chain rule for total derivatives implies a chain rule for partial derivatives. Recall that when the total derivative exists, the partial derivative in the ith coordinate direction is found by multiplying the Jacobian matrix by the ith basis vector. By doing this to the formula above, we find:

Since the entries of the Jacobian matrix are partial derivatives, we may simplify the above formula to get:

More conceptually, this rule expresses the fact that a change in the xi direction may change all of g1 through gk, and any of these changes may affect f.

In the special case where k = 1, so that f is a real-valued function, then this formula simplifies even further:

Read more about this topic:  Chain Rule

Famous quotes containing the words chain, rule, higher and/or dimensions:

    “The conclusion suggested by these arguments might be called the paradox of theorizing. It asserts that if the terms and the general principles of a scientific theory serve their purpose, i. e., if they establish the definite connections among observable phenomena, then they can be dispensed with since any chain of laws and interpretive statements establishing such a connection should then be replaceable by a law which directly links observational antecedents to observational consequents.”
    —C.G. (Carl Gustav)

    “Better the rule of One, whom all obey,
    Than to let clamorous demagogues betray
    Our freedom with the kiss of anarchy.”
    —Oscar Wilde (1854–1900)

    “For human nature, being more highly pitched, selved, and distinctive than anything in the world, can have been developed, evolved, condensed, from the vastness of the world not anyhow or by the working of common powers but only by one of finer or higher pitch and determination than itself.”
    —Gerard Manley Hopkins (1844–1889)

    “Is it true or false that Belfast is north of London? That the galaxy is the shape of a fried egg? That Beethoven was a drunkard? That Wellington won the battle of Waterloo? There are various degrees and dimensions of success in making statements: the statements fit the facts always more or less loosely, in different ways on different occasions for different intents and purposes.”
    —J.L. (John Langshaw)