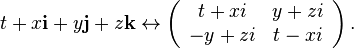Central Simple Algebra

In ring theory and related areas of mathematics a central simple algebra (CSA) over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K. In other words, any simple algebra is a central simple algebra over its center.

For example, the complex numbers C form a CSA over themselves, but not over the real numbers R (the center of C is all of C, not just R). The quaternions H form a 4 dimensional CSA over R, and in fact represent the only non-trivial element of the Brauer group of the reals (see below).

CSAs over a field K are a non-commutative analog to extension fields over K – in both cases, they have no non-trivial 2-sided ideals, and have a distinguished field in their center, though a CSA can be non-commutative and need not have inverses (need not be a division algebra). This is of particular interest in noncommutative number theory as generalizations of number fields (extensions of the rationals Q); see noncommutative number field.

According to the Artin–Wedderburn theorem a finite-dimensional simple algebra A is isomorphic to the matrix algebra M(n,S) for some division ring S.

Given two central simple algebras A ~ M(n,S) and B ~ M(m,T) over the same field F, A and B are called similar (or Brauer equivalent) if their division rings S and T are isomorphic. The set of all equivalence classes of central simple algebras over a given field F, under this equivalence relation, can be equipped with a group operation given by the tensor product of algebras. The resulting group is called the Brauer group Br(F) of the field F. It is always a torsion group.

We call a field E a splitting field for A if A⊗E is isomorphic to a matrix ring over E. Every finite dimensional CSA has a splitting field: indeed, in the case when A is a division algebra, then a maximal subfield of A is a splitting field. As an example, the field C splits the quaternion algebra H over R with

We can use the existence of the splitting field to define reduced norm and reduced trace for a CSA A. Map A to a matrix ring over a splitting field and define the reduced norm and trace to be the composite of this map with determinant and trace respectively. For example, in the quaternion algebra H, the element t + x i + y j + z k has reduced norm t2 + x2 + y2 + z2 and reduced trace 2t.