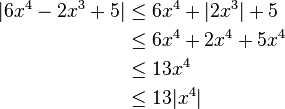Big O Notation - Example

Example

In typical usage, the formal definition of O notation is not used directly; rather, the O notation for a function f(x) is derived by the following simplification rules:

• If f(x) is a sum of several terms, the one with the largest growth rate is kept, and all others omitted.
• If f(x) is a product of several factors, any constants (terms in the product that do not depend on x) are omitted.

For example, let, and suppose we wish to simplify this function, using O notation, to describe its growth rate as x approaches infinity. This function is the sum of three terms: 6x4, −2x3, and 5. Of these three terms, the one with the highest growth rate is the one with the largest exponent as a function of x, namely 6x4. Now one may apply the second rule: 6x4 is a product of 6 and x4 in which the first factor does not depend on x. Omitting this factor results in the simplified form x4. Thus, we say that f(x) is a big-oh of (x4) or mathematically we can write f(x) = O(x4). One may confirm this calculation using the formal definition: let f(x) = 6x4 − 2x3 + 5 and g(x) = x4. Applying the formal definition from above, the statement that f(x) = O(x4) is equivalent to its expansion,

for some suitable choice of x₀ and M and for all x > x₀. To prove this, let x₀ = 1 and M = 13. Then, for all x > x₀:

so