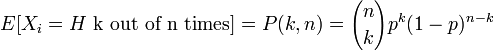Bernoulli Process - Binomial Distribution

Binomial Distribution

The law of large numbers states that, on average, the expectation value of flipping heads for any one coin flip is p. That is, one writes

for any one given random variable out of the infinite sequence of Bernoulli trials that compose the Bernoulli process.

One is often interested in knowing how often one will observe H in a sequence of n coin flips. This is given by simply counting: Given n successive coin flips, that is, given the set of all possible strings of length n, the number N(k,n) of such strings that contain k occurrences of H is given by the binomial coefficient

If the probability of flipping heads is given by p, then the total probability of seeing a string of length n with k heads is

This probability is known as the Binomial distribution.

Of particular interest is the question of the value of P(k,n) for very, very long sequences of coin flips, that is, for the limit . In this case, one may make use of Stirling's approximation to the factorial, and write

Inserting this into the expression for P(k,n), one obtains the Gaussian distribution; this is the content of the central limit theorem, and this is the simplest example thereof.

The combination of the law of large numbers, together with the central limit theorem, leads to an interesting and perhaps surprising result: the asymptotic equipartition property. Put informally, one notes that, yes, over many coin flips, one will observe H exactly p fraction of the time, and that this corresponds exactly with the peak of the Gaussian. The asymptotic equipartition property essentially states that this peak is infinitely sharp, with infinite fall-off on either side. That is, given the set of all possible infinitely long strings of H and T occurring in the Bernoulli process, this set is partitioned into two: those strings that occur with probability 1, and those that occur with probability 0. This partitioning is known as the Kolmogorov 0-1 law.

The size of this set is interesting, also, and can be explicitly determined: the logarithm of it is exactly the entropy of the Bernoulli process. Once again, consider the set of all strings of length n. The size of this set is . Of these, only a certain subset are likely; the size of this set is for . By using Stirling's approximation, putting it into the expression for P(k,n), solving for the location and width of the peak, and finally taking one finds that

This value is the Bernoulli entropy entropy of a Bernoulli process. Here, H stands for entropy; do not confuse it with the same symbol H standing for heads.

von Neumann posed a curious question about the Bernoulli process: is it ever possible that a given process is isomorphic to another, in the sense of the isomorphism of dynamical systems? The question long defied analysis, but was finally and completely answered with the Ornstein isomorphism theorem. This breakthrough resulted in the understanding that the Bernoulli process is unique and universal; in a certain sense, it is the single most random process possible; nothing is 'more' random than the Bernoulli process (although one must be careful with this informal statement; certainly, systems that are mixing are, in a certain sense, 'stronger' than the Bernoulli process, which is merely ergodic but not mixing. However, such processes do not consist of independent random variables: indeed, many purely deterministic, non-random systems can be mixing).