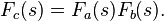Arithmetic Function - Dirichlet Convolution

Dirichlet Convolution

Given an arithmetic function a(n), let Fa(s), for complex s, be the function defined by the corresponding Dirichlet series (where it converges):

Fa(s) is called a generating function of a(n). The simplest such series, corresponding to the constant function a(n) = 1 for all n, is ς(s) the Riemann zeta function.

The generating function of the Möbius function is the inverse of the zeta function:

\zeta(s)\,\sum_{n=1}^\infty\frac{\mu(n)}{n^s}=1, \;\;\mathfrak{R} \,s >0.

Consider two arithmetic functions a and b and their respective generating functions Fa(s) and Fb(s). The product Fa(s)Fb(s) can be computed as follows:

It is a straightforward exercise to show that if c(n) is defined by

then

F_c(s) =F_a(s) F_b(s).\;

This function c is called the Dirichlet convolution of a and b, and is denoted by .

A particularly important case is convolution with the constant function a(n) = 1 for all n, corresponding to multiplying the generating function by the zeta function:

g(n) = \sum_{d|n}f(d).\;

Multiplying by the inverse of the zeta function gives the Möbius inversion formula:

f(n) = \sum_{d|n}\mu\left(\frac{n}{d}\right)g(d).

If f is multiplicative, then so is g. If f is completely multiplicative, then g is multiplicative, but may or may not be completely multiplicative. The article multiplicative function has a short proof.

Read more about this topic:  Arithmetic Function