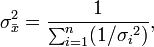Weighted Mean - Dealing With Variance

Dealing With Variance

See also: Least squares#Weighted least squares See also: Linear least squares (mathematics)#Weighted linear least squares

For the weighted mean of a list of data for which each element comes from a different probability distribution with known variance, one possible choice for the weights is given by:

$w_i = \frac{1}{\sigma_i^2}.$

The weighted mean in this case is:

$\bar{x} = \frac{ \sum_{i=1}^n (x_i/{\sigma_i}^2)}{\sum_{i=1}^n (1/{\sigma_i}^2)},$

and the variance of the weighted mean is:

$\sigma_{\bar{x}}^2 = \frac{ 1 }{\sum_{i=1}^n (1/{\sigma_i}^2)},$

which reduces to, when all

The significance of this choice is that this weighted mean is the maximum likelihood estimator of the mean of the probability distributions under the assumption that they are independent and normally distributed with the same mean.

Read more about this topic: Weighted Mean

Famous quotes containing the words dealing with, dealing and/or variance:

“Undecidability is a useful category even in dealing with restaurant menus.”
—Mason Cooley (b. 1927)

“The economic dependence of woman and her apparently indestructible illusion that marriage will release her from loneliness and work and worry are potent factors in immunizing her from common sense in dealing with men at work.”
—Mary Barnett Gilson (1877–?)

“There is an untroubled harmony in everything, a full consonance in nature; only in our illusory freedom do we feel at variance with it.”
—Fyodor Tyutchev (1803–1873)