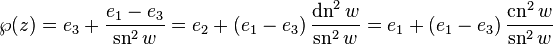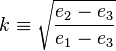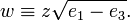Weierstrass's Elliptic Functions - Relation To Jacobi Elliptic Functions

Relation To Jacobi Elliptic Functions

For numerical work, it is often convenient to calculate the Weierstrass elliptic function in terms of the Jacobi's elliptic functions. The basic relations are

\wp(z) = e_{3} + \frac{e_{1} - e_{3}}{\mathrm{sn}^{2}\,w} = e_{2} + \left( e_{1} - e_{3} \right) \frac{\mathrm{dn}^{2}\,w}{\mathrm{sn}^{2}\,w} = e_{1} + \left( e_{1} - e_{3} \right) \frac{\mathrm{cn}^{2}\,w}{\mathrm{sn}^{2}\,w}

where e1-3 are the three roots described above and where the modulus k of the Jacobi functions equals

k \equiv \sqrt{\frac{e_{2} - e_{3}}{e_{1} - e_{3}}}

and their argument w equals

w \equiv z \sqrt{e_{1} - e_{3}}.

Read more about this topic:  Weierstrass's Elliptic Functions

Famous quotes containing the words relation to, relation, jacobi and/or functions:

    “Whoever has a keen eye for profits, is blind in relation to his craft.”
    —Sophocles (497–406/5 B.C.)

    “Parents ought, through their own behavior and the values by which they live, to provide direction for their children. But they need to rid themselves of the idea that there are surefire methods which, when well applied, will produce certain predictable results. Whatever we do with and for our children ought to flow from our understanding of and our feelings for the particular situation and the relation we wish to exist between us and our child.”
    —Bruno Bettelheim (20th century)

    “... the most important effect of the suffrage is psychological. The permanent consciousness of power for effective action, the knowledge that their own thoughts have an equal chance with those of any other person ... this is what has always rendered the men of a free state so energetic, so acutely intelligent, so powerful.”
    —Mary Putnam Jacobi (1842–1906)

    “In today’s world parents find themselves at the mercy of a society which imposes pressures and priorities that allow neither time nor place for meaningful activities and relations between children and adults, which downgrade the role of parents and the functions of parenthood, and which prevent the parent from doing things he wants to do as a guide, friend, and companion to his children.”
    —Urie Bronfenbrenner (b. 1917)