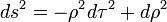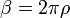Calculations
The theory of the Unruh effect involves the Rindler coordinates and, which have metric
This is just ordinary Minkowski space in relativistic polar coordinates:
The orbit in (1+1) space-time is a regular hyperbola. The parametric equations are of the above form, but with equal to the ratio of square of the speed of light to the proper acceleration. It is therefore a constant. There is only one parameter - the proper time . In the arguments of the hyperbolic function, this should be multiplied by the ratio of the proper acceleration to the speed of light.
A detector moving along a path of constant is uniformly accelerated, and is coupled to field modes which have a definite steady frequency as a function of . These modes are constantly Doppler shifted relative to ordinary Minkowski time as the detector accelerates, and they change in frequency by enormous factors, even after only a short proper time.
Translation in is a symmetry of Minkowski space: It is a boost around the origin. For a detector coupled to modes with a definite frequency in, the boost operator is then the Hamiltonian. In the Euclidean field theory, these boosts analytically continue to rotations, and the rotations close after . So
The path integral for this Hamiltonian is closed with period which guarantees that the H modes are thermally occupied with temperature . This is not an actual temperature, because H is dimensionless. It is conjugate to the timelike polar angle which is also dimensionless. To restore the length dimension, note that a mode of fixed frequency f in at position has a frequency which is determined by the square root of the metric at, the redshift factor. The actual inverse temperature at this point is therefore
Since the acceleration of a trajectory at constant is equal to, the actual inverse temperature observed is:
The temperature observed by a uniformly accelerating particle is (in engineering units):
The Unruh effect could only be seen when the Rindler horizon is visible. If a refrigerated accelerating wall is placed between the particle and the horizon, at fixed Rindler coordinate, the thermal boundary condition for the field theory at is the temperature of the wall. By making the positive side of the wall colder, the extension of the wall's state to is also cold. In particular, there is no thermal radiation from the acceleration of the surface of the Earth, nor for a detector accelerating in a circle, because under these circumstances there is no Rindler horizon in the field of view.
The temperature of the vacuum, seen by an isolated observer accelerated at the Earth's gravitational acceleration of g = 9.81 m/s², is only 4×10−20 K. For an experimental test of the Unruh effect it is planned to use accelerations up to 1026 m/s², which would give a temperature of about 400,000 K.
To put this in perspective, at a vacuum Unruh temperature of 3.978×10−20 K, an electron would have a de Broglie Wavelength of h/√(3mekT) = 540.85 meters, and a proton at that temperature would have a wavelength of 12.62 meters. If electrons and protons were in intimate contact in a very cold vacuum, they would have rather long wavelengths and interaction distances.
At one astronomical unit from the sun, the acceleration is GM s/AU² = 0.005932 m/s². This gives an Unruh temperature of 2.41×10−23 kelvin. At that temperature, the electron and proton wavelengths are 21.994 kilometers 513 meters, respectively. Even a uranium atom will have a wavelength of 2.2 meters at such a low temperature.
Read more about this topic: Unruh Effect
Famous quotes containing the word calculations:
“Now, since our condition accommodates things to itself, and transforms them according to itself, we no longer know things in their reality; for nothing comes to us that is not altered and falsified by our Senses. When the compass, the square, and the rule are untrue, all the calculations drawn from them, all the buildings erected by their measure, are of necessity also defective and out of plumb. The uncertainty of our senses renders uncertain everything that they produce.”
—Michel de Montaigne (1533–1592)
“Heaven’s calculations don’t follow man’s calculations.”
—Chinese proverb.
“What, really, is wanted from a neighborhood? Convenience, certainly, an absence of major aggravation, to be sure. But perhaps most of all, ideally, what is wanted is a comfortable background, a breathing space of intermission between the intensities of private life and the calculations of public life.”
—Joseph Epstein (b. 1937)