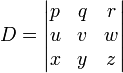Formulas
Trilinears enable many algebraic methods in triangle geometry. For example, three points
- P = p : q : r
- U = u : v : w
- X = x : y : z
are collinear if and only if the determinant
equals zero. The dual of this proposition is that the lines
- pα + qβ + rγ = 0
- uα + vβ + wγ = 0,
- xα + yβ + zγ = 0
concur in a point if and only if D = 0.
Also, if the actual directed distances are used when evaluating determinant D, then (area of (PUX)) = KD, where K = abc/8σ2 if triangle PUX has the same orientation as triangle ABC, and K = - abc/8σ2 otherwise.
Many cubic curves are easily represented using trilinears. For example, the pivotal self-isoconjugate cubic Z(U,P), as the locus of a point X such that the P-isoconjugate of X is on the line UX is given by the determinant equation
Among named cubics Z(U,P) are the following:
- Thomson cubic: Z(X(2),X(1)), where X(2) = centroid, X(1) = incenter
- Feuerbach cubic: Z(X(5),X(1)), where X(5) = Feuerbach point
- Darboux cubic: Z(X(20),X(1)), where X(20) = De Longchamps point
- Neuberg cubic: Z(X(30),X(1)), where X(30) = Euler infinity point.
Read more about this topic: Trilinear Coordinates
Famous quotes containing the word formulas:
“That’s the great danger of sectarian opinions, they always accept the formulas of past events as useful for the measurement of future events and they never are, if you have high standards of accuracy.”
—John Dos Passos (1896–1970)
“It is sentimentalism to assume that the teaching of life can always be fitted to the child’s interests, just as it is empty formalism to force the child to parrot the formulas of adult society. Interests can be created and stimulated.”
—Jerome S. Bruner (20th century)
“You treat world history as a mathematician does mathematics, in which nothing but laws and formulas exist, no reality, no good and evil, no time, no yesterday, no tomorrow, nothing but an eternal, shallow, mathematical present.”
—Hermann Hesse (1877–1962)