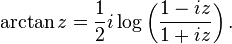Trigonometric Functions - Inverse Functions

Inverse Functions

The trigonometric functions are periodic, and hence not injective, so strictly they do not have an inverse function. Therefore to define an inverse function we must restrict their domains so that the trigonometric function is bijective. In the following, the functions on the left are defined by the equation on the right; these are not proved identities. The principal inverses are usually defined as:

Function Definition Value Field

The notations sin−1 and cos−1 are often used for arcsin and arccos, etc. When this notation is used, the inverse functions could be confused with the multiplicative inverses of the functions. The notation using the "arc-" prefix avoids such confusion, though "arcsec" can be confused with "arcsecond".

Just like the sine and cosine, the inverse trigonometric functions can also be defined in terms of infinite series. For example,

\arcsin z = z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots\,.

These functions may also be defined by proving that they are antiderivatives of other functions. The arcsine, for example, can be written as the following integral:

\arcsin z = \int_0^z (1 - x^2)^{-1/2}\,dx, \quad |z| < 1.

Analogous formulas for the other functions can be found at Inverse trigonometric functions. Using the complex logarithm, one can generalize all these functions to complex arguments:

\arcsin z = -i \log \left( i z + \sqrt{1 - z^2} \right), \,
\arccos z = -i \log \left( z + \sqrt{z^2 - 1}\right), \,
\arctan z = \frac12i \log\left(\frac{1-iz}{1+iz}\right).

Read more about this topic:  Trigonometric Functions

Famous quotes containing the words inverse and/or functions:

    “Yet time and space are but inverse measures of the force of the soul. The spirit sports with time.”
    —Ralph Waldo Emerson (1803–1882)

    “Nobody is so constituted as to be able to live everywhere and anywhere; and he who has great duties to perform, which lay claim to all his strength, has, in this respect, a very limited choice. The influence of climate upon the bodily functions ... extends so far, that a blunder in the choice of locality and climate is able not only to alienate a man from his actual duty, but also to withhold it from him altogether, so that he never even comes face to face with it.”
    —Friedrich Nietzsche (1844–1900)