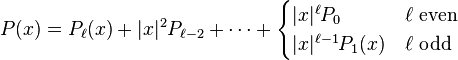Spherical Harmonics - Higher Dimensions

Higher Dimensions

The classical spherical harmonics are defined as functions on the unit sphere S2 inside three-dimensional Euclidean space. Spherical harmonics can be generalized to higher dimensional Euclidean space Rn as follows. Let Pℓ denote the space of homogeneous polynomials of degree ℓ in n variables. That is, a polynomial P is in Pℓ provided that

Let Aℓ denote the subspace of Pℓ consisting of all harmonic polynomials; these are the solid spherical harmonics. Let Hℓ denote the space of functions on the unit sphere

obtained by restriction from Aℓ.

The following properties hold:

  • The spaces Hℓ are dense in the set of continuous functions on Sn−1 with respect to the uniform topology, by the Stone-Weierstrass theorem. As a result, they are also dense in the space L2(Sn−1) of square-integrable functions on the sphere.
  • For all ƒ ∈ Hℓ, one has
where ΔSn−1 is the Laplace–Beltrami operator on Sn−1. This operator is the analog of the angular part of the Laplacian in three dimensions; to wit, the Laplacian in n dimensions decomposes as
  • It follows from the Stokes theorem and the preceding property that the spaces Hℓ are orthogonal with respect to the inner product from L2(Sn−1). That is to say,
for ƒ ∈ Hℓ and g ∈ Hk for k ≠ ℓ.
  • Conversely, the spaces Hℓ are precisely the eigenspaces of ΔSn−1. In particular, an application of the spectral theorem to the Riesz potential gives another proof that the spaces Hℓ are pairwise orthogonal and complete in L2(Sn−1).
  • Every homogeneous polynomial P ∈ Pℓ can be uniquely written in the form
P(x) = P_\ell(x) + |x|^2P_{\ell-2} + \cdots + \begin{cases} |x|^\ell P_0 & \ell \rm{\ even}\\ |x|^{\ell-1} P_1(x) & \ell\rm{\ odd} \end{cases}
where Pj ∈ Aj. In particular,

An orthogonal basis of spherical harmonics in higher dimensions can be constructed inductively by the method of separation of variables, by solving the Sturm-Liouville problem for the spherical Laplacian

where φ is the axial coordinate in a spherical coordinate system on Sn−1. The end result of such a procedure is

Y_{l_1, \dots l_{n-1}} (\theta_1, \dots \theta_{n-1}) = \frac{1}{\sqrt{2\pi}} e^{i l_1 \theta_1} \prod_{j = 2}^{n-1} {}_j \bar{P}^{l_{n-1} - 1}_{l_j} (\theta_j)

where the indices satisfy |ℓ1| ≤ ℓ2 ≤ ... ≤ ℓn−1 and the eigenvalue is −ℓn−1(ℓn−1 + n−2). The functions in the product are defined in terms of the Legendre function

{}_j \bar{P}^l_{L} (\theta) = \sqrt{\frac{2L+j-1}{2} \frac{(L+l+j-2)!}{(L-l)!}} \sin^{\frac{2-j}{2}} (\theta) P^{-(l + \frac{j-2}{2})}_{L+\frac{j-2}{2}} (\cos \theta)

Read more about this topic:  Spherical Harmonics

Famous quotes containing the words higher and/or dimensions:

    “The higher we rise up, the smaller we appear to those who are unable to fly.”
    —Friedrich Nietzsche (1844–1900)

    “I was surprised by Joe’s asking me how far it was to the Moosehorn. He was pretty well acquainted with this stream, but he had noticed that I was curious about distances, and had several maps. He and Indians generally, with whom I have talked, are not able to describe dimensions or distances in our measures with any accuracy. He could tell, perhaps, at what time we should arrive, but not how far it was.”
    —Henry David Thoreau (1817–1862)