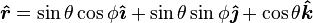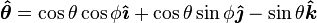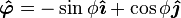Spherical Coordinate System - Integration and Differentiation in Spherical Coordinates

Integration and Differentiation in Spherical Coordinates

The following equations assume that θ is inclination from the normal axis:

The line element for an infinitesimal displacement from to is

where

\boldsymbol{\hat r} =\sin \theta \cos \phi \boldsymbol{\hat{\imath}} + \sin \theta \sin \phi \boldsymbol{\hat{\jmath}} + \cos \theta \boldsymbol{\hat{k}}
\boldsymbol{\hat\theta } =\cos \theta \cos \phi\boldsymbol{\hat{\imath}} + \cos \theta \sin \phi \boldsymbol{\hat{\jmath}} -\sin \theta \boldsymbol{\hat{k}}
\boldsymbol{\hat \varphi} =-\sin \phi \boldsymbol{\hat{\imath}} + \cos \phi \boldsymbol{\hat{\jmath}}

are the local orthogonal unit vectors in the directions of increasing, respectively.

The surface element spanning from to and to on a spherical surface at (constant) radius is

Thus the differential solid angle is

The surface element in a surface of polar angle constant (a cone with vertex the origin) is

The surface element in a surface of azimuth constant (a vertical half-plane) is

The volume element spanning from to, to, and to is

Thus, for example, a function can be integrated over every point in R3 by the triple integral

The del operator in this system is not defined, and so the gradient, divergence and curl must be defined explicitly:

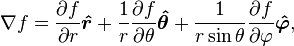
\nabla f={\partial f \over \partial r}\boldsymbol{\hat r} + {1 \over r}{\partial f \over \partial \theta}\boldsymbol{\hat \theta} + {1 \over r\sin\theta}{\partial f \over \partial \varphi}\boldsymbol{\hat \varphi},

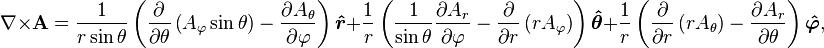
\nabla \times \mathbf{A} = \displaystyle{1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( A_\varphi\sin\theta \right) - {\partial A_\theta \over \partial \varphi}\right) \boldsymbol{\hat r} + \displaystyle{1 \over r}\left({1 \over \sin\theta}{\partial A_r \over \partial \varphi} - {\partial \over \partial r} \left( r A_\varphi \right) \right) \boldsymbol{\hat \theta} + \displaystyle{1 \over r}\left({\partial \over \partial r} \left( r A_\theta \right) - {\partial A_r \over \partial \theta}\right) \boldsymbol{\hat \varphi},

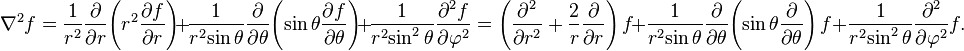
\nabla^2 f={1 \over r^2}{\partial \over \partial r}\!\left(r^2 {\partial f \over \partial r}\right) \!+\!{1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!+\!{1 \over r^2\!\sin^2\theta}{\partial^2 f \over \partial \varphi^2} = \left(\frac{\partial^2}{\partial r^2} + \frac{2}{r} \frac{\partial}{\partial r}\right)f \!+ {1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta \frac{\partial}{\partial \theta}\right)f +\frac{1}{r^2\!\sin^2\theta}\frac{\partial^2}{\partial \varphi^2}f.

Read more about this topic:  Spherical Coordinate System

Famous quotes containing the words integration and and/or integration:

    “Look back, to slavery, to suffrage, to integration and one thing is clear. Fashions in bigotry come and go. The right thing lasts.”
    —Anna Quindlen (b. 1952)

    “The more specific idea of evolution now reached is—a change from an indefinite, incoherent homogeneity to a definite, coherent heterogeneity, accompanying the dissipation of motion and integration of matter.”
    —Herbert Spencer (1820–1903)