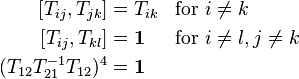Special Linear Group - Generators and Relations

Generators and Relations

If working over a ring where SL is generated by transvections (such as a field or Euclidean domain), one can give a presentation of SL using transvections with some relations. Transvections satisfy the Steinberg relations, but these are not sufficient: the resulting group is the Steinberg group, which is not the special linear group, but rather the universal central extension of the commutator subgroup of GL.

A sufficient set of relations for SL(n, Z) for n ≥ 3 is given by two of the Steinberg relations, plus a third relation (Conder, Robertson & Williams 1992, p. 19). Let Tij := eij(1) be the elementary matrix with 1's on the diagonal and in the ij position, and 0's elsewhere (and i ≠ j). Then

\begin{align} \left &= T_{ik} && \mbox{for } i \neq k\\ \left &= \mathbf{1} && \mbox{for } i \neq l, j \neq k\\ (T_{12}T_{21}^{-1}T_{12})^4 &= \mathbf{1}\\ \end{align}

are a complete set of relations for SL(n, Z), n ≥ 3.

Read more about this topic:  Special Linear Group

Famous quotes containing the word relations:

    “When one walks, one is brought into touch first of all with the essential relations between one’s physical powers and the character of the country; one is compelled to see it as its natives do. Then every man one meets is an individual. One is no longer regarded by the whole population as an unapproachable and uninteresting animal to be cheated and robbed.”
    —Aleister Crowley (1875–1947)