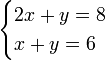A Simple Example
This is a set of linear equations, also known as a linear system of equations:
Solving this involves subtracting x + y = 6 from 2x + y = 8 (using the elimination method) to remove the y-variable, then simplifying the resulting equation to find the value of x, then substituting the x-value into either equation to find y.
The solution of this system is:
which can also be written as an ordered pair (2, 4), representing on a graph the coordinates of the point of intersection of the two lines represented by the equations.
Read more about this topic: Simultaneous Equations
Famous quotes containing the word simple:
“When I think of God, when I think of him as existent, and when I believe him to be existent, my idea of him neither increases nor diminishes. But as it is certain there is a great difference betwixt the simple conception of the existence of an object, and the belief of it, and as this difference lies not in the parts or composition of the idea which we conceive; it follows, that it must lie in the manner in which we conceive it.”
—David Hume (1711–1776)