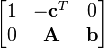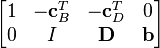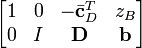Simplex Algorithm - Canonical Tableaux

Canonical Tableaux

A linear program in standard form can be represented as a tableau of the form

\begin{bmatrix} 1 & -\mathbf{c}^T & 0 \\ 0 & \mathbf{A} & \mathbf{b} \end{bmatrix}

The first row defines the objective function and the remaining rows specify the constraints. (Note, different authors use different conventions as to the exact layout.) If the columns of A can be rearranged so that it contains the identity matrix of order p (the number of rows in A) then the tableau is said to be in canonical form. The variables corresponding to the columns of the identity matrix are called basic variables while the remaining variables are called nonbasic or free variables. If the nonbasic variables are assumed to be 0, then the values of the basic variables are easily obtained as entries in b and this solution is a basic feasible solution.

Conversely, given a basic feasible solution, the columns corresponding to the nonzero variables can be expanded to a nonsingular matrix. If the corresponding tableau is multiplied by the inverse of this matrix then the result is a tableau in canonical form.

Let

\begin{bmatrix} 1 & -\mathbf{c}^T_B & -\mathbf{c}^T_D & 0 \\ 0 & I & \mathbf{D} & \mathbf{b} \end{bmatrix}

be a tableau in canonical form. Additional row-addition transformations can be applied to remove the coefficients cTB from the objective function. This process is called pricing out and results in a canonical tableau

\begin{bmatrix} 1 & 0 & -\bar{\mathbf{c}}^T_D & z_B \\ 0 & I & \mathbf{D} & \mathbf{b} \end{bmatrix}

where zB is the value of the objective function at the corresponding basic feasible solution. The updated coefficients, also known as relative cost coefficients, are the rates of change of the objective function with respect to the nonbasic variables.

Read more about this topic:  Simplex Algorithm

Famous quotes containing the word canonical:

    “If God bestowed immortality on every man then when he made him, and he made many to whom he never purposed to give his saving grace, what did his Lordship think that God gave any man immortality with purpose only to make him capable of immortal torments? It is a hard saying, and I think cannot piously be believed. I am sure it can never be proved by the canonical Scripture.”
    —Thomas Hobbes (1579–1688)