Shear Rate - Simple Shear

Simple Shear

The shear rate for a fluid flowing between two parallel plates, one moving at a constant speed and the other one stationary (Couette flow), is defined by

where

  • = The shear rate, measured in reciprocal seconds
  • = The velocity of the moving plate, measured in meters per second
  • = The distance between the two parallel plates, measured in meters

Or, 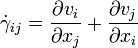\dot \gamma_{ij}=\frac {\partial v_i} {\partial x_j} + \frac{\partial v_j} {\partial x_i}

For the simple shear case, it is just a gradient of velocity in a flowing material. The SI unit of measurement for shear rate is s-1, expressed as "reciprocal seconds" or "inverse seconds."

The shear rate at the inner wall of a Newtonian fluid flowing within a pipe is:

where:

  • = The shear rate, measured in reciprocal seconds.
  • = The linear fluid velocity.
  • = The inside diameter of the pipe.

The linear fluid velocity v is related to the volumetric flow rate Q by:

where A is the cross-sectional area of the pipe, which for an inside pipe radius of r is given by:

thus producing:

Substituting the above into the earlier equation for the shear rate of a Newtonian fluid flowing within a pipe, and noting (in the denominator) that d = 2r:

which simplifies to the following equivalent form for wall shear rate in terms of volumetric flow rate Q and inner pipe radius r :


For a Newtonian fluid wall shear stress can be related to shear rate by, where is the viscosity of the fluid. For Non-Newtonian fluids, there are different constitutive laws depending on the fluid, which relates the stress tensor to the shear rate tensor.

Read more about this topic:  Shear Rate

Famous quotes containing the word simple:

    “But the whim we have of happiness is somewhat thus. By certain valuations, and averages, of our own striking, we come upon some sort of average terrestrial lot; this we fancy belongs to us by nature, and of indefeasible rights. It is simple payment of our wages, of our deserts; requires neither thanks nor complaint.... Foolish soul! What act of legislature was there that thou shouldst be happy? A little while ago thou hadst no right to be at all.”
    —Thomas Carlyle (1795–1881)