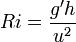The Richardson number is named after Lewis Fry Richardson (1881 – 1953). It is the dimensionless number that expresses the ratio of potential to kinetic energy
where g is the acceleration due to gravity, h a representative vertical lengthscale, and u a representative speed.
When considering flows in which density differences are small (the Boussinesq approximation), it is common to use the reduced gravity g' and the relevant parameter is the densimetric Richardson number
which is used frequently when considering atmospheric or oceanic flows.
If the Richardson number is much less than unity, buoyancy is unimportant in the flow. If it is much greater than unity, buoyancy is dominant (in the sense that there is insufficient kinetic energy to homogenize the fluids).
If the Richardson number is of order unity, then the flow is likely to be buoyancy-driven: the energy of the flow derives from the potential energy in the system originally.
Read more about Richardson Number: Aviation, Thermal Convection, Oceanography
Famous quotes containing the words richardson and/or number:
“What a world is this! What is there in it desirable? The good we hope for so strangely mixed, that one knows not what to wish for! And one half of mankind tormenting the other, and being tormented themselves in tormenting!”
—Samuel Richardson (1689–1761)
“But however the forms of family life have changed and the number expanded, the role of the family has remained constant and it continues to be the major institution through which children pass en route to adulthood.”
—Bernice Weissbourd (20th century)