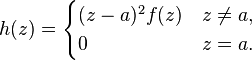Removable Singularity - Riemann's Theorem

Riemann's Theorem

Riemann's theorem on removable singularities states when a singularity is removable:

Theorem. Let be an open subset of the complex plane, a point of and a holomorphic function defined on the set . The following are equivalent:

1. is holomorphically extendable over .
2. is continuously extendable over .
3. There exists a neighborhood of on which is bounded.
4. .

The implications 1 ⇒ 2 ⇒ 3 ⇒ 4 are trivial. To prove 4 ⇒ 1, we first recall that the holomorphy of a function at is equivalent to it being analytic at (proof), i.e. having a power series representation. Define

Clearly, h is holomorphic on D \ {a}, and there exists

by 4, hence h is holomorphic on D and has a Taylor series about a:

We have c₀ = h(a) = 0 and c₁ = h'(a) = 0; therefore

is a holomorphic extension of f over a, which proves the claim.