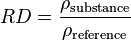Relative Density - Basic Formulas

Basic Formulas

Relative density (RD) or specific gravity (SG) is a dimensionless quantity, as it is the ratio of either densities or weights

where RD is relative density, ρ_substance is the density of the substance being measured, and ρ_reference is the density of the reference. (By convention ρ, the Greek letter rho, denotes density.)

The reference material can be indicated using subscripts: RD_{substance/reference}, which means "the relative density of substance with respect to reference". If the reference is not explicitly stated then it is normally assumed to be water at 4 °C (or, more precisely, 3.98 °C, which is the temperature at which water reaches its maximum density). In SI units, the density of water is (approximately) 1000 kg/m3 or 1 g/cm3, which makes relative density calculations particularly convenient: the density of the object only needs to be divided by 1000 or 1, depending on the units.

The relative density of gases is often measured with respect to dry air at a temperature of 20 °C and a pressure of 101.325 kPa absolute, which has a density of 1.205 kg/m3. Relative density with respect to air can be obtained by

Where M is the molar mass and the approximately equal sign is used because equality pertains only if 1 mol of the gas and 1 mol of air occupy the same volume at a given temperature and pressure i.e. they are both Ideal gases. Ideal behaviour is usually only seen at very low pressure. For example, one mol of an ideal gas occupies 22.414 L at 0 °C and 1 atmosphere whereas carbon dioxide has a molar volume of 22.259 L under those same conditions.