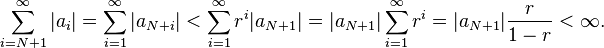Ratio Test - Proof

Proof

Below is a proof of the validity of the original ratio test.

Suppose that . We can then show that the series converges absolutely by showing that its terms will eventually become less than those of a certain convergent geometric series. To do this, let . Then r is strictly between L and 1, and for sufficiently large n (say, n greater than N). Hence for each n > N and i > 0, and so

$\sum_{i=N+1}^{\infty}|a_{i}| = \sum_{i=1}^{\infty}|a_{N+i}| < \sum_{i=1}^{\infty}r^{i}|a_{N+1}| = |a_{N+1}|\sum_{i=1}^{\infty}r^{i} = |a_{N+1}|\frac{r}{1 - r} < \infty.$

That is, the series converges absolutely.

On the other hand, if L > 1, then for sufficiently large n, so that the limit of the summands is non-zero. Hence the series diverges.

Famous quotes containing the word proof:

“The insatiable thirst for everything which lies beyond, and which life reveals, is the most living proof of our immortality.”
—Charles Baudelaire (1821–1867)

“O, popular applause! what heart of man
Is proof against thy sweet, seducing charms?”
—William Cowper (1731–1800)

“He who has never failed somewhere, that man can not be great. Failure is the true test of greatness. And if it be said, that continual success is a proof that a man wisely knows his powers,—it is only to be added, that, in that case, he knows them to be small.”
—Herman Melville (1819–1891)