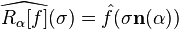Radon Transform - Relationship With The Fourier Transform

Relationship With The Fourier Transform

The Radon transform is closely related to the Fourier transform. For a function of one variable the Fourier transform is defined by

\hat{f}(\omega)=\int_{-\infty}^\infty f(x)e^{-2\pi ix\omega }\,dx.

and for a function of a 2-vector ,

\hat{f}(\mathbf{w})=\int\limits_{-\infty}^{\infty} \int\limits_{-\infty }^{\infty} f(\mathbf{x})e^{-2\pi i\mathbf{x}\cdot\mathbf{w}}\,dx\, dy.

For convenience define as it is only meaningful to take the Fourier transform in the variable. The Fourier slice theorem then states

\widehat{R_{\alpha}}(\sigma)=\hat{f}(\sigma\mathbf{n}(\alpha))

where

Thus the two-dimensional Fourier transform of the initial function is the one variable Fourier transform of the Radon transform of that function. More generally, one has the result valid in n dimensions

Indeed, the result follows at once by computing the two variable Fourier integral along appropriate slices:

An application of the Fourier inversion formula also gives an explicit inversion formula for the Radon transform, and thus shows that it is invertible on suitably chosen spaces of functions. However this form is not particularly useful for numerical inversion, and faster discrete inversion methods exist.

Read more about this topic:  Radon Transform

Famous quotes containing the words relationship with the, relationship and/or transform:

    “Christianity as an organized religion has not always had a harmonious relationship with the family. Unlike Judaism, it kept almost no rituals that took place in private homes. The esteem that monasticism and priestly celibacy enjoyed implied a denigration of marriage and parenthood.”
    —Beatrice Gottlieb, U.S. historian. The Family in the Western World from the Black Death to the Industrial Age, ch. 12, Oxford University Press (1993)

    “We think of religion as the symbolic expression of our highest moral ideals; we think of magic as a crude aggregate of superstitions. Religious belief seems to become mere superstitious credulity if we admit any relationship with magic. On the other hand our anthropological and ethnographical material makes it extremely difficult to separate the two fields.”
    —Ernst Cassirer (1874–1945)

    “God defend me from that Welsh fairy,
    Lest he transform me to a piece of cheese!”
    —William Shakespeare (1564–1616)