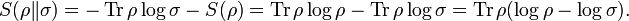Definition
As with many other objects in quantum information theory, quantum relative entropy is defined by extending the classical definition from probability distributions to density matrices. Let ρ be a density matrix. The von Neumann entropy of ρ, which is the quantum mechanical analog of the Shannon entropy, is given by
For two density matrices ρ and σ, the quantum relative entropy of ρ with respect to σ is defined by
We see that, when the states are classical, i.e. ρσ = σρ, the definition coincides with the classical case.
Read more about this topic: Quantum Relative Entropy
Famous quotes containing the word definition:
“Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
—The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)
“Beauty, like all other qualities presented to human experience, is relative; and the definition of it becomes unmeaning and useless in proportion to its abstractness. To define beauty not in the most abstract, but in the most concrete terms possible, not to find a universal formula for it, but the formula which expresses most adequately this or that special manifestation of it, is the aim of the true student of aesthetics.”
—Walter Pater (1839–1894)
“... if, as women, we accept a philosophy of history that asserts that women are by definition assimilated into the male universal, that we can understand our past through a male lens—if we are unaware that women even have a history—we live our lives similarly unanchored, drifting in response to a veering wind of myth and bias.”
—Adrienne Rich (b. 1929)