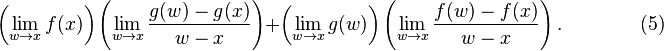Product Rule - Proof of The Product Rule

Proof of The Product Rule

A rigorous proof of the product rule can be given using the properties of limits and the definition of the derivative as a limit of Newton's difference quotient.

If

and ƒ and g are each differentiable at the fixed number x, then

Now the difference

is the area of the big rectangle minus the area of the small rectangle in the illustration.

The region between the smaller and larger rectangle can be split into two rectangles, the sum of whose areas is

Therefore the expression in (1) is equal to

Assuming that all limits used exist, (4) is equal to

\left(\lim_{w\to x}f(x)\right) \left(\lim_{w\to x} {g(w) - g(x) \over w - x}\right) + \left(\lim_{w\to x} g(w)\right) \left(\lim_{w\to x} {f(w) - f(x) \over w - x} \right). \qquad\qquad(5)

Now

This holds because f(x) remains constant as w → x.

This holds because differentiable functions are continuous (g is assumed differentiable in the statement of the product rule).

Also:

and

because f and g are differentiable at x;

We conclude that the expression in (5) is equal to

Read more about this topic:  Product Rule

Famous quotes containing the words proof of, proof, product and/or rule:

    “Sculpture and painting are very justly called liberal arts; a lively and strong imagination, together with a just observation, being absolutely necessary to excel in either; which, in my opinion, is by no means the case of music, though called a liberal art, and now in Italy placed even above the other two—a proof of the decline of that country.”
    —Philip Dormer Stanhope, 4th Earl Chesterfield (1694–1773)

    “To cease to admire is a proof of deterioration.”
    —Charles Horton Cooley (1864–1929)

    “[The political mind] is a strange mixture of vanity and timidity, of an obsequious attitude at one time and a delusion of grandeur at another time. The political mind is the product of men in public life who have been twice spoiled. They have been spoiled with praise and they have been spoiled with abuse.”
    —Calvin Coolidge (1872–1933)

    “The condition that gives birth to a rule is not the same as the condition to which the rule gives birth.”
    —Friedrich Nietzsche (1844–1900)