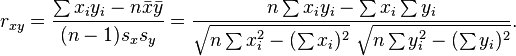Pearson Product-moment Correlation Coefficient - Mathematical Properties

Mathematical Properties

The absolute value of both the sample and population Pearson correlation coefficients are less than or equal to 1. Correlations equal to 1 or -1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).

A key mathematical property of the Pearson correlation coefficient is that it is invariant (up to a sign) to separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants, without changing the correlation coefficient (this fact holds for both the population and sample Pearson correlation coefficients). Note that more general linear transformations do change the correlation: see a later section for an application of this.

The Pearson correlation can be expressed in terms of uncentered moments. Since μX = E(X), σX2 = E = E(X2) − E2(X) and likewise for Y, and since

the correlation can also be written as

Alternative formulae for the sample Pearson correlation coefficient are also available:

r_{xy}=\frac{\sum x_iy_i-n \bar{x} \bar{y}}{(n-1) s_x s_y}=\frac{n\sum x_iy_i-\sum x_i\sum y_i} {\sqrt{n\sum x_i^2-(\sum x_i)^2}~\sqrt{n\sum y_i^2-(\sum y_i)^2}}.

The above formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes be numerically unstable.

Read more about this topic:  Pearson Product-moment Correlation Coefficient

Famous quotes containing the words mathematical and/or properties:

    “An accurate charting of the American woman’s progress through history might look more like a corkscrew tilted slightly to one side, its loops inching closer to the line of freedom with the passage of time—but like a mathematical curve approaching infinity, never touching its goal. . . . Each time, the spiral turns her back just short of the finish line.”
    —Susan Faludi (20th century)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)