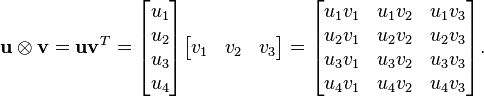Outer Product - Definition (matrix Multiplication)

Definition (matrix Multiplication)

The outer product u ⊗ v is equivalent to a matrix multiplication uvT, provided that u is represented as a m × 1 column vector and v as a n × 1 column vector (which makes vT a row vector). For instance, if m = 4 and n = 3, then

\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^T = \begin{bmatrix}u_1 \\ u_2 \\ u_3 \\ u_4\end{bmatrix} \begin{bmatrix}v_1 & v_2 & v_3\end{bmatrix} = \begin{bmatrix}u_1v_1 & u_1v_2 & u_1v_3 \\ u_2v_1 & u_2v_2 & u_2v_3 \\ u_3v_1 & u_3v_2 & u_3v_3 \\ u_4v_1 & u_4v_2 & u_4v_3\end{bmatrix}.

For complex vectors, it is customary to use the conjugate transpose of v (denoted vH):

Read more about this topic:  Outer Product

Famous quotes containing the word definition:

    “One definition of man is “an intelligence served by organs.””
    —Ralph Waldo Emerson (1803–1882)