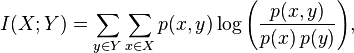Mutual Information - Definition of Mutual Information

Definition of Mutual Information

Formally, the mutual information of two discrete random variables X and Y can be defined as:

I(X;Y) = \sum_{y \in Y} \sum_{x \in X} p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)} \right) }, \,\!

where p(x,y) is the joint probability distribution function of X and Y, and and are the marginal probability distribution functions of X and Y respectively.

In the case of continuous random variables, the summation is replaced by a definite double integral:

I(X;Y) = \int_Y \int_X p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)} \right) } \; dx \,dy,

where p(x,y) is now the joint probability density function of X and Y, and and are the marginal probability density functions of X and Y respectively.

These definitions are ambiguous because the base of the log function is not specified. To disambiguate, the function I could be parameterized as I(X,Y,b) where b is the base. Alternatively, since the most common unit of measurement of mutual information is the bit, a base of 2 could be specified.

Intuitively, mutual information measures the information that X and Y share: it measures how much knowing one of these variables reduces uncertainty about the other. For example, if X and Y are independent, then knowing X does not give any information about Y and vice versa, so their mutual information is zero. At the other extreme, if X and Y are identical then all information conveyed by X is shared with Y: knowing X determines the value of Y and vice versa. As a result, in the case of identity the mutual information is the same as the uncertainty contained in Y (or X) alone, namely the entropy of Y (or X: clearly if X and Y are identical they have equal entropy).

Mutual information is a measure of the inherent dependence expressed in the joint distribution of X and Y relative to the joint distribution of X and Y under the assumption of independence. Mutual information therefore measures dependence in the following sense: I(X; Y) = 0 if and only if X and Y are independent random variables. This is easy to see in one direction: if X and Y are independent, then p(x,y) = p(x) p(y), and therefore:

\log{ \left( \frac{p(x,y)}{p(x)\,p(y)} \right) } = \log 1 = 0. \,\!

Moreover, mutual information is nonnegative (i.e. I(X;Y) ≥ 0; see below) and symmetric (i.e. I(X;Y) = I(Y;X)).

Read more about this topic:  Mutual Information

Famous quotes containing the words definition of, definition, mutual and/or information:

    “The physicians say, they are not materialists; but they are:MSpirit is matter reduced to an extreme thinness: O so thin!—But the definition of spiritual should be, that which is its own evidence. What notions do they attach to love! what to religion! One would not willingly pronounce these words in their hearing, and give them the occasion to profane them.”
    —Ralph Waldo Emerson (1803–1882)

    “The physicians say, they are not materialists; but they are:MSpirit is matter reduced to an extreme thinness: O so thin!—But the definition of spiritual should be, that which is its own evidence. What notions do they attach to love! what to religion! One would not willingly pronounce these words in their hearing, and give them the occasion to profane them.”
    —Ralph Waldo Emerson (1803–1882)

    “True love does not quarrel for slight reasons, such mistakes as mutual acquaintances can explain away, but, alas, however slight the apparent cause, only for adequate and fatal and everlasting reasons, which can never be set aside.”
    —Henry David Thoreau (1817–1862)

    “Information networks straddle the world. Nothing remains concealed. But the sheer volume of information dissolves the information. We are unable to take it all in.”
    —Günther Grass (b. 1927)