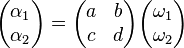Modular Group - Number-theoretic Properties

Number-theoretic Properties

The unit determinant of

implies that the fractions a/b, a/c, c/d and b/d are all irreducible, that is have no common factors (provided the denominators are non-zero, of course). More generally, if is an irreducible fraction, then

\frac{ap+bq}{cp+dq}

is also irreducible (again, provided the denominator be non-zero). Any pair of irreducible fractions can be connected in this way, i.e.: for any pair p/q and r/s of irreducible fractions, there exist elements

such that

Elements of the modular group provide a symmetry on the two-dimensional lattice. Let and be two complex numbers whose ratio is not real. Then the set of points is a lattice of parallelograms on the plane. A different pair of vectors and will generate exactly the same lattice if and only if

\begin{pmatrix}\alpha_1 \\ \alpha_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix}

for some matrix in . It is for this reason that doubly periodic functions, such as elliptic functions, possess a modular group symmetry.

The action of the modular group on the rational numbers can most easily be understood by envisioning a square grid, with grid point (p,q) corresponding to the fraction p/q (see Euclid's orchard). An irreducible fraction is one that is visible from the origin; the action of the modular group on a fraction never takes a visible (irreducible) to a hidden (reducible) one, and vice versa.

If and are two successive convergents of a continued fraction, then the matrix

belongs to . In particular, if bc − ad = 1 for positive integers a,b,c and d with a < b and c < d then a⁄b and c⁄d will be neighbours in the Farey sequence of order min(b,d). Important special cases of continued fraction convergents include the Fibonacci numbers and solutions to Pell's equation. In both cases, the numbers can be arranged to form a semigroup subset of the modular group.

Read more about this topic:  Modular Group

Famous quotes containing the word properties:

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)