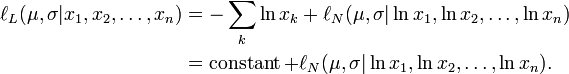Log-normal Distribution - Maximum Likelihood Estimation of Parameters

Maximum Likelihood Estimation of Parameters

For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that

where by ƒL we denote the probability density function of the log-normal distribution and by ƒN that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:

\begin{align} \ell_L (\mu,\sigma | x_1, x_2, \dots, x_n) & {} = - \sum _k \ln x_k + \ell_N (\mu, \sigma | \ln x_1, \ln x_2, \dots, \ln x_n) \\ & {} = \operatorname {constant} + \ell_N (\mu, \sigma | \ln x_1, \ln x_2, \dots, \ln x_n). \end{align}

Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, ℓL and ℓN, reach their maximum with the same μ and σ. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that

\widehat \mu = \frac {\sum_k \ln x_k} n, \widehat \sigma^2 = \frac {\sum_k \left( \ln x_k - \widehat \mu \right)^2} {n}.

Read more about this topic:  Log-normal Distribution

Famous quotes containing the words maximum, likelihood, estimation and/or parameters:

    “Only at his maximum does an individual surpass all his derivative elements, and become purely himself. And most people never get there. In his own pure individuality a man surpasses his father and mother, and is utterly unknown to them.”
    —D.H. (David Herbert)

    “Sustained unemployment not only denies parents the opportunity to meet the food, clothing, and shelter needs of their children but also denies them the sense of adequacy, belonging, and worth which being able to do so provides. This increases the likelihood of family problems and decreases the chances of many children to be adequately prepared for school.”
    —James P. Comer (20th century)

    “A higher class, in the estimation and love of this city- building, market-going race of mankind, are the poets, who, from the intellectual kingdom, feed the thought and imagination with ideas and pictures which raise men out of the world of corn and money, and console them for the short-comings of the day, and the meanness of labor and traffic.”
    —Ralph Waldo Emerson (1803–1882)

    “What our children have to fear is not the cars on the highways of tomorrow but our own pleasure in calculating the most elegant parameters of their deaths.”
    —J.G. (James Graham)