Lists of Integrals - Definite Integrals Lacking Closed-form Antiderivatives

Definite Integrals Lacking Closed-form Antiderivatives

There are some functions whose antiderivatives cannot be expressed in closed form. However, the values of the definite integrals of some of these functions over some common intervals can be calculated. A few useful integrals are given below.

(see also Gamma function)
(the Gaussian integral)
for a > 0
\int_0^\infty x^{2n} e^{-a x^2}\,dx = \frac{2n-1}{2a} \int_0^\infty x^{2(n-1)} e^{-a x^2}\,dx = \frac{(2n-1)!!}{2^{n+1}} \sqrt{\frac{\pi}{a^{2n+1}}} = \frac{(2n)!}{n! 2^{2n+1}} \sqrt{\frac{\pi}{a^{2n+1}}} for a > 0, n is 1, 2, 3, ... and !! is the double factorial.
when a > 0
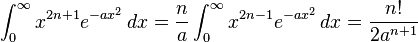\int_0^\infty x^{2n+1} e^{-a x^2}\,dx = \frac {n} {a} \int_0^\infty x^{2n-1} e^{-a x^2}\,dx = \frac{n!}{2 a^{n+1}} for a > 0, n = 0, 1, 2, ....
(see also Bernoulli number)
(see sinc function and Sine integral)
(if n is an even integer and )
(if is an odd integer and )
\int_{-\pi}^\pi \cos(\alpha x)\cos^n(\beta x) dx = \begin{cases} \frac{2 \pi}{2^n} \binom{n}{m} & |\alpha|= |\beta (2m-n)| \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
(for real and non-negative integer, see also Symmetry)
\int_{-\pi}^\pi \sin(\alpha x) \sin^n(\beta x) dx = \begin{cases} (-1)^{(n+1)/2} (-1)^m \frac{2 \pi}{2^n} \binom{n}{m} & n \text{ odd},\ \alpha = \beta (2m-n) \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
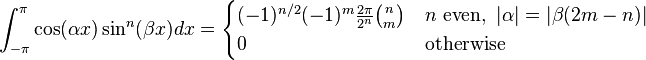\int_{-\pi}^{\pi} \cos(\alpha x) \sin^n(\beta x) dx = \begin{cases} (-1)^{n/2} (-1)^m \frac{2 \pi}{2^n} \binom{n}{m} & n \text{ even},\ |\alpha| = |\beta (2m-n)| \\ 0 & \text{otherwise} \end{cases} (for integers with and, see also Binomial coefficient)
(where is the exponential function, and )
(where is the Gamma function)
(the Beta function)
(where is the modified Bessel function of the first kind)
, this is related to the probability density function of the Student's t-distribution)

The method of exhaustion provides a formula for the general case when no antiderivative exists:

(Click "show" at right to see a proof or "hide" to hide it.)

Read more about this topic:  Lists Of Integrals

Famous quotes containing the words definite and/or lacking:

    “... life cannot be administered by definite rules and regulations; that wisdom to deal with a man’s difficulties comes only through some knowledge of his life and habits as a whole ...”
    —Jane Addams (1860–1935)

    “Chippenhook was the home of Judge Theophilus Harrington, known for his trenchant reply to an irate slave-owner in a runaway slave case. Judge Harrington declared that the owner’s claim to the slave was defective. The owner indignantly demanded to know what was lacking in his legally sound claim. The Judge exploded, ‘A bill of sale, sir, from God Almighty!’”
    —For the State of Vermont, U.S. public relief program (1935-1943)