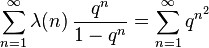Lambert Series - Examples

Examples

Since this last sum is a typical number-theoretic sum, almost any natural multiplicative function will be exactly summable when used in a Lambert series. Thus, for example, one has

where is the number of positive divisors of the number n.

For the higher order sigma functions, one has

where is any complex number and

is the divisor function.

Lambert series in which the an are trigonometric functions, for example, an = sin(2n x), can be evaluated by various combinations of the logarithmic derivatives of Jacobi theta functions.

Other Lambert series include those for the Möbius function :

For Euler's totient function :

For Liouville's function :

\sum_{n=1}^\infty \lambda(n)\,\frac{q^n}{1-q^n} = \sum_{n=1}^\infty q^{n^2}

with the sum on the left similar to the Ramanujan theta function.

Read more about this topic:  Lambert Series

Famous quotes containing the word examples:

    “There are many examples of women that have excelled in learning, and even in war, but this is no reason we should bring ‘em all up to Latin and Greek or else military discipline, instead of needle-work and housewifry.”
    —Bernard Mandeville (1670–1733)

    “It is hardly to be believed how spiritual reflections when mixed with a little physics can hold people’s attention and give them a livelier idea of God than do the often ill-applied examples of his wrath.”
    —G.C. (Georg Christoph)

    “In the examples that I here bring in of what I have [read], heard, done or said, I have refrained from daring to alter even the smallest and most indifferent circumstances. My conscience falsifies not an iota; for my knowledge I cannot answer.”
    —Michel de Montaigne (1533–1592)