Jacobi Symbol - Properties

Properties

These facts, even the reciprocity laws, are straightforward deductions from the definition of the Jacobi symbol and the corresponding properties of the Legendre symbol.

It should be noted that the Jacobi symbol is only defined when the upper argument ("numerator") is an integer and the lower argument ("denominator") is a positive odd integer.

1) If is (an odd) prime, then the Jacobi symbol is also a Legendre symbol.
2) If then
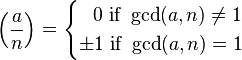
3) \left(\frac{a}{n}\right) = \begin{cases} \;\;\,0\mbox{ if } \gcd(a,n) \ne 1 \\\pm1\mbox{ if } \gcd(a,n) = 1\end{cases}
4), so (or )
5), so (or )

The law of quadratic reciprocity: if m and n are odd positive coprime integers, then

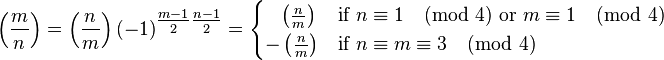
6) \left(\frac{m}{n}\right) = \left(\frac{n}{m}\right)(-1)^{\tfrac{m-1}{2}\tfrac{n-1}{2}} = \begin{cases} \;\;\;\left(\frac{n}{m}\right) & \text{if }n \equiv 1 \pmod 4 \text{ or } m \equiv 1 \pmod 4 \\ -\left(\frac{n}{m}\right) & \text{if }n\equiv m \equiv 3 \pmod 4 \end{cases}

and its supplements

7) \left(\frac{-1}{n}\right) = (-1)^\tfrac{n-1}{2} = \begin{cases} \;\;\,1 & \text{if }n \equiv 1 \pmod 4\\ -1 &\text{if }n \equiv 3 \pmod 4\end{cases}
8) \left(\frac{2}{n}\right) = (-1)^\tfrac{n^2-1}{8} = \begin{cases} \;\;\,1 & \text{if }n \equiv 1,7 \pmod 8\\ -1 &\text{if }n \equiv 3,5\pmod 8\end{cases}

Like the Legendre symbol,

If then is a quadratic nonresidue
If is a quadratic residue then

But, unlike the Legendre symbol

If then may or may not be a quadratic residue .

This is because for a to be a residue (mod n) it has to be a residue modulo every prime that divides n, but the Jacobi symbol will equal one if for example a is a non-residue for exactly two of the primes which divide n.

Although the Jacobi symbol can't be uniformly interpreted in terms of squares and non-squares, it can be uniformly interpreted as the sign of a permutation by Zolotarev's lemma.

The Jacobi symbol is a Dirichlet character to the modulus n.

Read more about this topic:  Jacobi Symbol

Famous quotes containing the word properties:

    “The reason why men enter into society, is the preservation of their property; and the end why they choose and authorize a legislative, is, that there may be laws made, and rules set, as guards and fences to the properties of all the members of the society: to limit the power, and moderate the dominion, of every part and member of the society.”
    —John Locke (1632–1704)

    “A drop of water has the properties of the sea, but cannot exhibit a storm. There is beauty of a concert, as well as of a flute; strength of a host, as well as of a hero.”
    —Ralph Waldo Emerson (1803–1882)