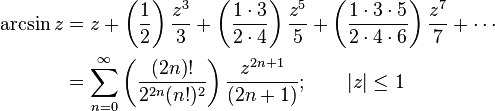Inverse Trigonometric Functions - Infinite Series

Infinite Series

Like the sine and cosine functions, the inverse trigonometric functions can be calculated using infinite series, as follows:

\begin{align} \arcsin z & {}= z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots\\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1 \end{align}


\begin{align} \arccos z & {}= \frac {\pi} {2} - \arcsin z \\ & {}= \frac {\pi} {2} - (z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1 \end{align}


\begin{align} \arctan z & {}= z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots \\ & {}= \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i \end{align}


\begin{align} \arccot z & {}= \frac {\pi} {2} - \arctan z \\ & {}= \frac {\pi} {2} - ( z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i \end{align}


\begin{align} \arcsec z & {}= \arccos {(1/z)} \\ & {}= \frac {\pi} {2} - (z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^{-5}} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^{-7}} {7} + \cdots ) \\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {(2n+1)} ; \qquad \left| z \right| \ge 1 \end{align}


\begin{align} \arccsc z & {}= \arcsin {(1/z)} \\ & {}= z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4 } \right) \frac {z^{-5}} {5} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {z^{-7}} {7} +\cdots \\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {2n+1} ; \qquad \left| z \right| \ge 1 \end{align}


Leonhard Euler found a more efficient series for the arctangent, which is:

(Notice that the term in the sum for n= 0 is the empty product which is 1.)


Alternatively, this can be expressed:

Read more about this topic:  Inverse Trigonometric Functions

Famous quotes containing the words infinite series, infinite and/or series:

    “In the order of literature, as in others, there is no act that is not the coronation of an infinite series of causes and the source of an infinite series of effects.”
    —Jorge Luis Borges (1899–1986)

    “Age cannot wither her, nor custom stale
    Her infinite variety. Other women cloy
    The appetites they feed, but she makes hungry
    Where most she satisfies.”
    —William Shakespeare (1564–1616)

    “Every man sees in his relatives, and especially in his cousins, a series of grotesque caricatures of himself.”
    —H.L. (Henry Lewis)