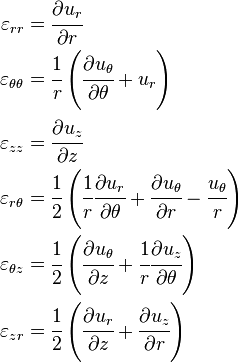Infinitesimal Strain Theory - Strain Tensor in Cylindrical Coordinates

Strain Tensor in Cylindrical Coordinates

In cylindrical polar coordinates, the displacement vector can be written as

\mathbf{u} = u_r~\mathbf{e}_r + u_\theta~\mathbf{e}_\theta + u_z~\mathbf{e}_z

The components of the strain tensor in a cylindrical coordinate system are given by

\begin{align} \varepsilon_{rr} & = \cfrac{\partial u_r}{\partial r} \\ \varepsilon_{\theta\theta} & = \cfrac{1}{r}\left(\cfrac{\partial u_\theta}{\partial \theta} + u_r\right) \\ \varepsilon_{zz} & = \cfrac{\partial u_z}{\partial z} \\ \varepsilon_{r\theta} & = \cfrac{1}{2}\left(\cfrac{1}{r}\cfrac{\partial u_r}{\partial \theta} + \cfrac{\partial u_\theta}{\partial r}- \cfrac{u_\theta}{r}\right) \\ \varepsilon_{\theta z} & = \cfrac{1}{2}\left(\cfrac{\partial u_\theta}{\partial z} + \cfrac{1}{r}\cfrac{\partial u_z}{\partial \theta}\right) \\ \varepsilon_{zr} & = \cfrac{1}{2}\left(\cfrac{\partial u_r}{\partial z} + \cfrac{\partial u_z}{\partial r}\right) \end{align}

Read more about this topic:  Infinitesimal Strain Theory

Famous quotes containing the word strain:

    “Finding everything deep—that is an inconvenient trait: it causes a person constantly to strain his eyes and eventually to find out more than he might have wished.”
    —Friedrich Nietzsche (1844–1900)