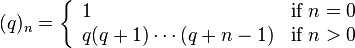Hypergeometric Function - The Hypergeometric Series

The Hypergeometric Series

The hypergeometric function is defined for |z| < 1 by the power series

provided that c does not equal 0, −1, −2, ... . Here (q)n is the Pochhammer symbol, which is defined by:

(q)_n = \left\{ \begin{array}{ll} 1 & \mbox{if } n = 0 \\ q(q+1) \cdots (q+n-1) & \mbox{if } n > 0 \end{array} \right .

Notice that the series terminates if either a or b is a nonpositive integer. For complex arguments z with |z| ≥ 1 it can be analytically continued along any path in the complex plane that avoids the branch points 0 and 1.

Read more about this topic:  Hypergeometric Function

Famous quotes containing the word series:

    “Autobiography is only to be trusted when it reveals something disgraceful. A man who gives a good account of himself is probably lying, since any life when viewed from the inside is simply a series of defeats.”
    —George Orwell (1903–1950)